过拟合问题 Overfitting
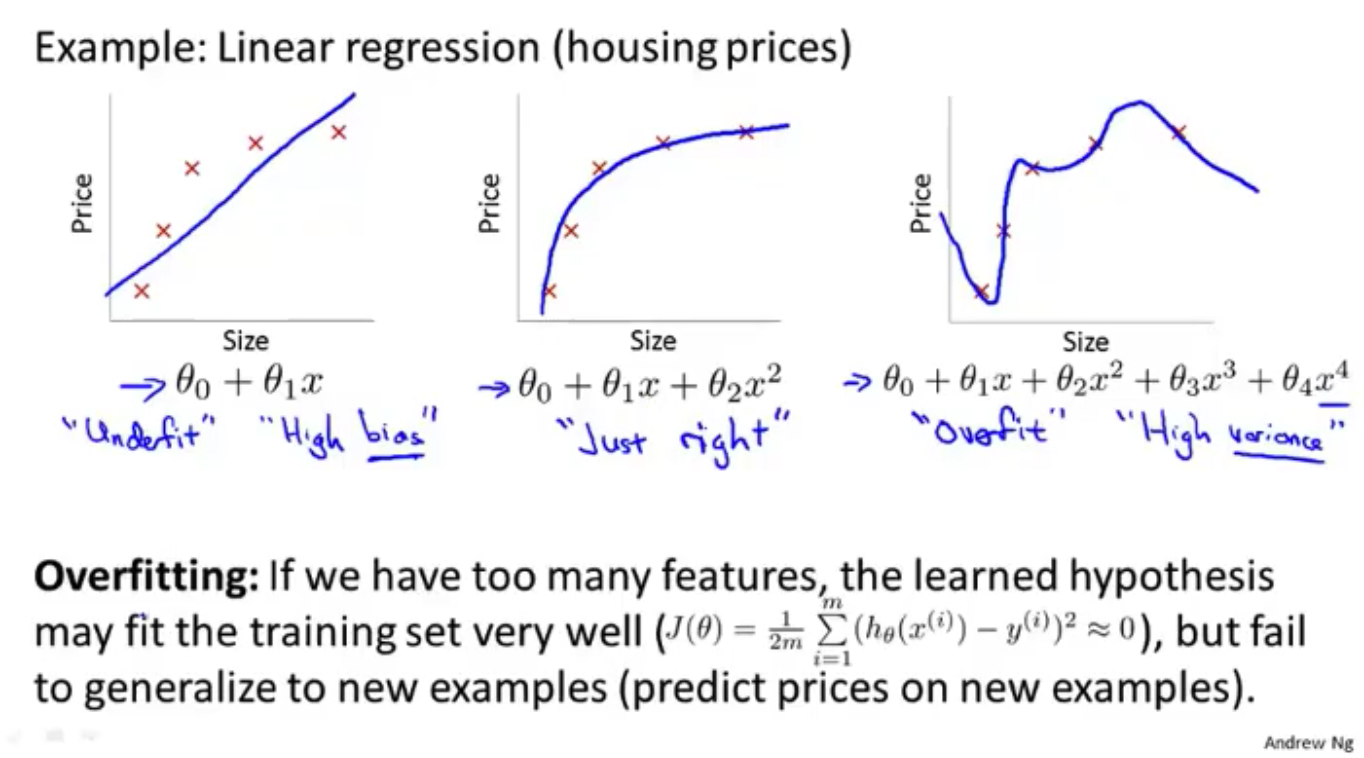
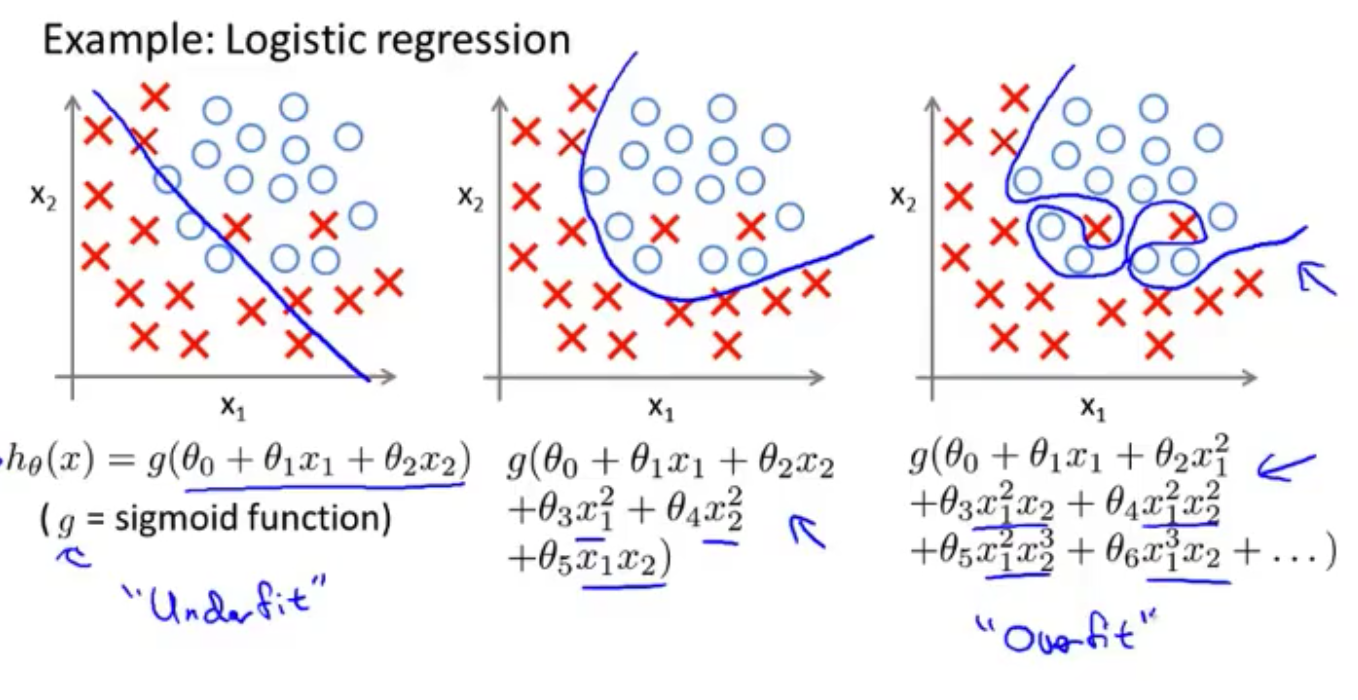
欠拟合 underfitting (high bias 高偏差)
过拟合 overfitting (high variance 高方差)
解决的办法
- 减少特征的数量
- 手动选择保留哪些特征
- 模型选择算法
- 正则化 Regularization
- 保留所有特征,但是减少量级或者参数 $\theta$ 的大小
- 当特征非常多的时候依旧非常有效,每一个特征都会对预测 $y$ 产生影响
代价函数
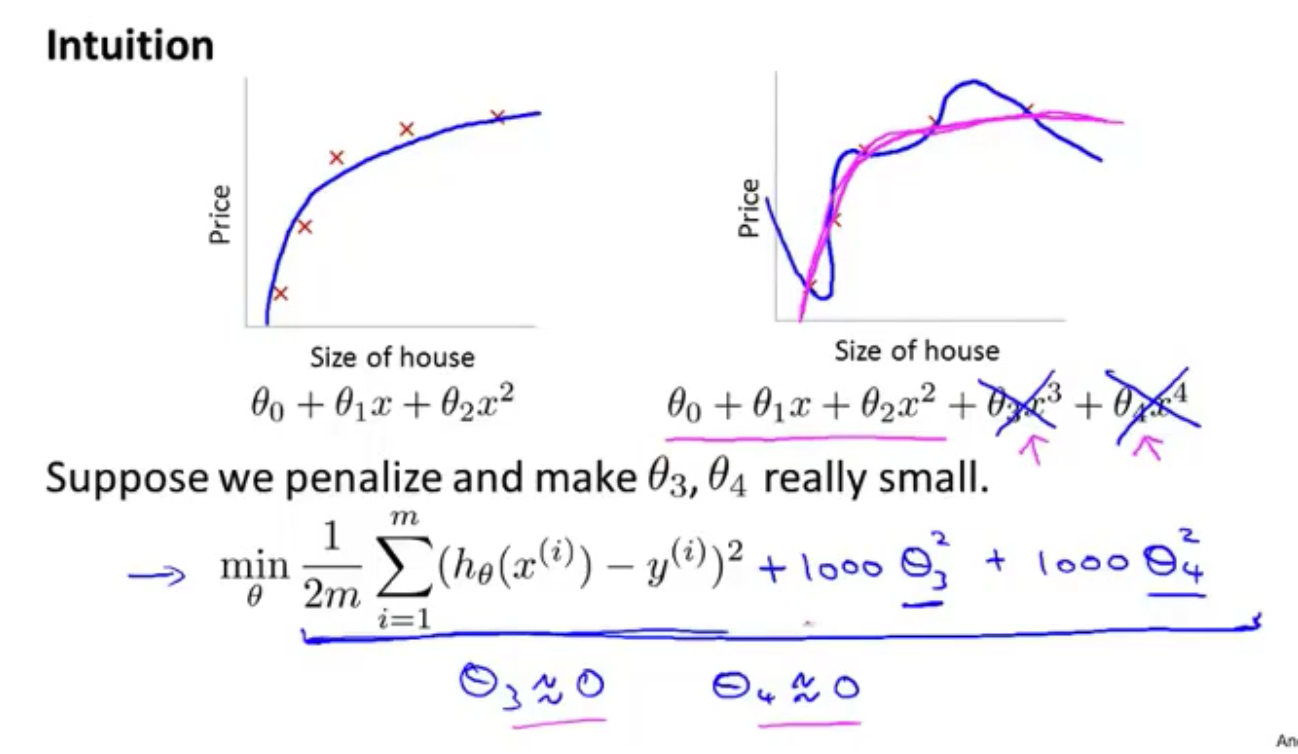
解决办法的思想
在 $\theta_3$ 和 $\theta_4$ 中增加惩罚,增加一个很大的数与之相乘,这样要最小化代价函数,最后 $\theta_3$ 和 $\theta_4$ 会变得非常小(接近于0),这样最后的结果得到了依旧类似于一个二次函数
Regularization
Small values for parameters $\theta_0$ , $\theta_1$ , … , $\theta_n$
- “Simpler”hypothsis 简化假设模型(如上面的解决方法)
- Less prone to overfitting 更不容易过拟合
实际运用中的做法
$J(\theta)=\frac{1}{2m}[\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum_{i=1}^{m}\theta_j^2]$
(虽然是从 $\theta_0$ 开始,但是实际使用从 $\theta_1$ 开始,效果并无二致)
后面的 $\lambda\sum_{i=1}^{m}\theta_j^2$ 被称作正则化项,$\lambda$ 是正则化参数
$\lambda$ 的作用就是控制以下两个目标的取舍:
- 使训练结果更好地拟合数据
- 降低每个 $\theta$ 的大小(正则化),避免过拟合

如果 $\lambda$ 设置的太大,会造成欠拟合,如上所示,可能会变成一条直线
线性回归的正则化
梯度下降
$J(\theta)=\frac{1}{2m}[\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum_{i=1}^{m}\theta_j^2]$
$\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum_{i=1}^{m}\theta_j^2$ 中的前半部分是线性回归的一般目标,后面部分是正则化项

$\theta_j(1-\alpha\frac{\lambda}{m})$ 将$\theta_j$向0的方向缩小的一点点(后面的参数一般是0.99这种靠近1的数字)
正规方程
$\theta=(X^TX)^{-1}X^Ty$
正则化后:


正则化还可以解决一些 $X^TX$ 不可逆的问题
逻辑回归的正则化
梯度下降法的正则化
$J(\theta)=\frac{1}{m}\sum_{i=1}^{m}Cost(h_\theta(x^{(i)}),y^{(i)})$
$=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)})log(1-h_\theta(x^{(i)}))]$
$h_\theta(x)=\frac{1}{1+e^{-\theta^{T}x}}$
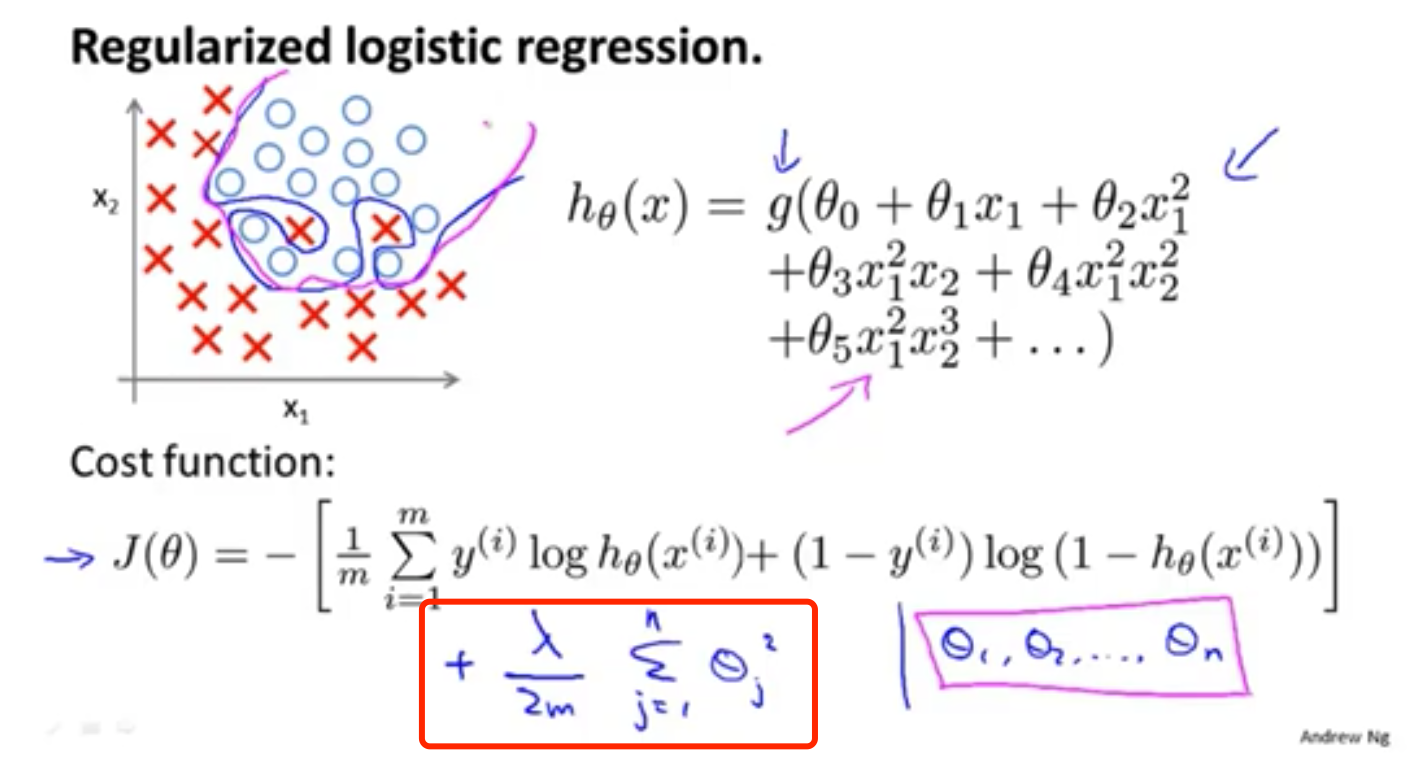
$J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}logh_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)}))]+\frac{\lambda}{2m}\sum_{j=1}^{n}\theta_j^2$
也是在后面增加正则项

与线性回归的正则化很相似
